Construction of Conic Section Curves/कोनिक सेक्शन कर्व्स का निर्माण

This article provides an introduction to construction of conic section curves. (Visit for Full Course or Watch Video Lecture here)

A cone is a surface formed by rotating a straight line with one end in contact with a fixed point and the other end in contact with a closed curve that does not lie in the curve’s plane.

एक शंकु एक सतह है जो एक निश्चित बिंदु के साथ संपर्क में एक छोर के साथ एक सीधी रेखा को घुमाकर और दूसरा छोर एक बंद वक्र के संपर्क में है जो वक्र के विमान में झूठ नहीं बोलता है।

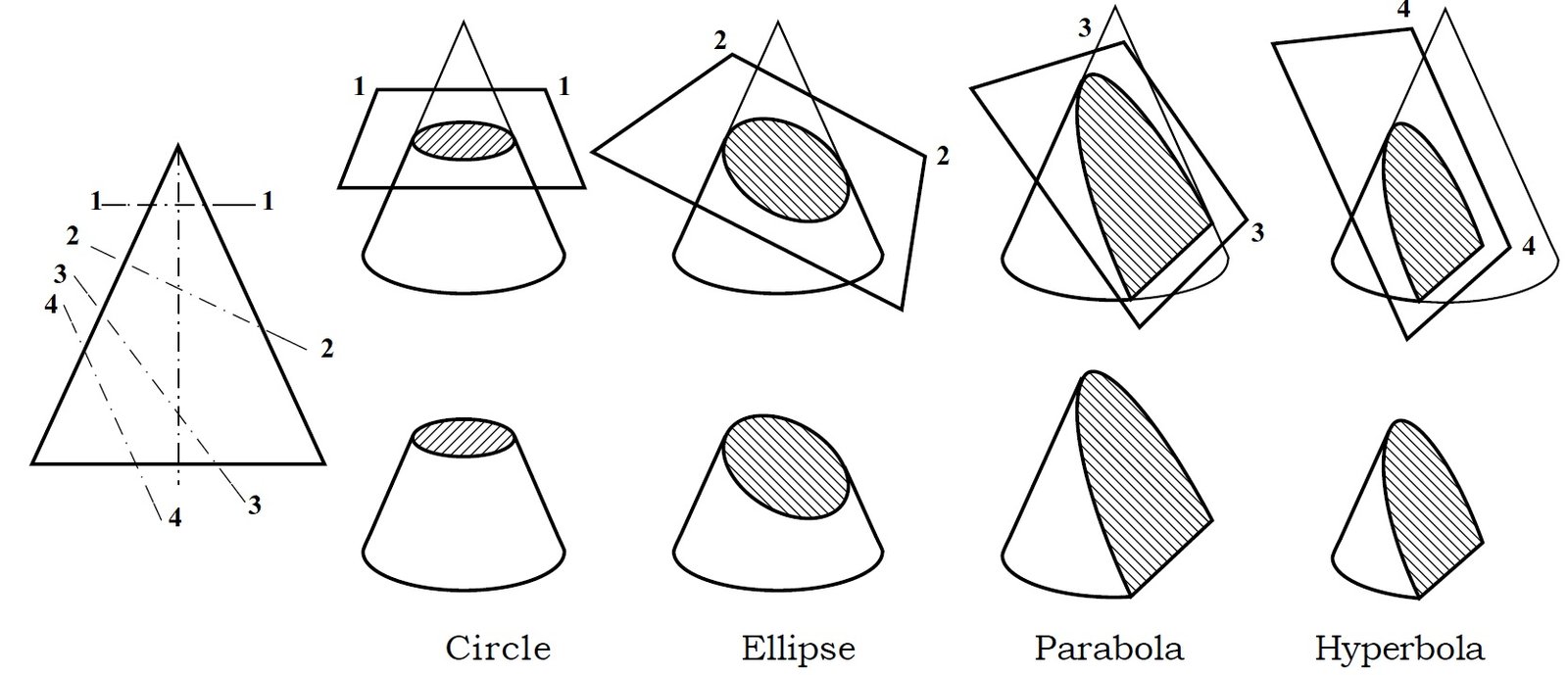
Conic sections are obtained by cutting off a right circular cone by section planes at varying angles relative to its axis.
Conic sections include the circle, ellipse, parabola, and hyperbola.
शंकु वर्गों को इसकी धुरी के सापेक्ष अलग -अलग कोणों पर अनुभाग विमानों द्वारा एक सही गोलाकार शंकु को काटकर प्राप्त किया जाता है।
शंकु वर्गों में सर्कल, दीर्घवृत्त, परबोला और हाइपरबोला शामिल हैं।

(i) Circle: A circle is formed when a cutting plane is perpendicular to the axis and cuts all of the generators.
(ii) Ellipse: An ellipse is formed when a cutting plane is inclined to the cone’s axis and cuts all of the generators on one side of the apex.
(iii) Parabola: The section obtained when a cutting plane is inclined to the axis of the cone and parallel to one of the generators is known as a parabola.
(iv) Hyperbola: A hyperbola section is formed when the cutting plane forms a smaller angle with the axis than the angle made by the cone’s generator.

(i) सर्कल: एक सर्कल तब बनता है जब एक काटने वाला विमान अक्ष के लंबवत होता है और सभी जनरेटर को काट देता है।
(ii) दीर्घवृत्त: एक दीर्घवृत्त तब बनता है जब एक काटने वाला विमान शंकु के अक्ष पर झुका होता है और शीर्ष के एक तरफ सभी जनरेटर को काट देता है।
(iii) परबोला: जब एक कटिंग प्लेन को शंकु के अक्ष के लिए झुकाया जाता है और जनरेटर में से एक के समानांतर होता है, तो उसे प्राप्त होता है।
(iv) हाइपरबोला: एक हाइपरबोला सेक्शन तब बनता है जब कटिंग प्लेन शंकु के जनरेटर द्वारा बनाए गए कोण की तुलना में अक्ष के साथ एक छोटा कोण बनाता है।

conic section curves

Various Terminology of Conic Section Curves / शंकु खंड वक्र की विभिन्न शब्दावली

(i) Conic section: A conic section is defined as the locus of a moving point in a plane such that the ratio of its distance from a fixed point to a fixed straight line is always a constant. This ratio is known as eccentricity (e).
(ii) Ellipse: An ellipse is the locus of a moving point in a plane whose distance from a fixed point to a fixed straight line is constant. It’s always 1.
(iii) Parabola: A point travelling in a plane whose distance from a fixed point to a fixed straight line is constant and always equals one.
(iv) Hyperbola: A hyperbola is the locus of a point travelling in a plane in such a way that the ratio of its distance from a fixed point to a fixed straight line is constant and greater than one.
(v) Focus: The fixed point is referred to as Focus.
(vi) Directrix: The fixed line is referred to as Directrix.
(vii) Axis: A line that passes through focus and is perpendicular to the directrix.
(viii) Vertex: A vertex is a point on the conic’s axis.
(ix) Eccentricity: e = (Distance of the moving point from the focus)/(Distance of the moving point from the directrix)

(Visit for Full Course or Watch Video Lecture here)

 

Terminology of Conic Section Curves

 

(i) शंकु खंड: एक शंकु खंड को एक विमान में एक चलती बिंदु के स्थान के रूप में परिभाषित किया जाता है जैसे कि एक निश्चित बिंदु से एक निश्चित सीधी रेखा तक इसकी दूरी का अनुपात हमेशा एक स्थिर होता है। इस अनुपात को सनकी (ई) के रूप में जाना जाता है।
(ii) दीर्घवृत्त: एक दीर्घवृत्त एक विमान में एक चलती बिंदु का स्थान है, जिसका एक निश्चित बिंदु से एक निश्चित सीधी रेखा की दूरी स्थिर है। यह हमेशा 1 है।
(iii) परबोला: एक विमान में यात्रा करने वाला एक बिंदु जिसका एक निश्चित बिंदु से एक निश्चित सीधी रेखा तक की दूरी स्थिर है और हमेशा एक के बराबर होती है।
(iv) हाइपरबोला: एक हाइपरबोला एक विमान में यात्रा करने वाले बिंदु का स्थान इस तरह से है कि एक निश्चित बिंदु से एक निश्चित सीधी रेखा तक इसकी दूरी का अनुपात स्थिर और एक से अधिक है।
(v) फोकस: फिक्स्ड पॉइंट को फोकस के रूप में संदर्भित किया जाता है।
(vi) Directrix: फिक्स्ड लाइन को डायरेक्ट्रिक्स के रूप में संदर्भित किया जाता है।
(vii) अक्ष: एक रेखा जो फोकस से गुजरती है और डायरेक्ट्रिक्स के लिए लंबवत होती है।
(viii) वर्टेक्स: एक वर्टेक्स शंकु के अक्ष पर एक बिंदु है।
(ix) विलक्षणता: ई = (फोकस से चलती बिंदु की दूरी)/(डायरेक्ट्रिक्स से चलती बिंदु की दूरी)

Construction of Ellipse / दीर्घवृत्त का निर्माण

Elliptical shapes are employed in the building of arches, bridges, dams, elliptical gears of textile machines and printing presses, the ends of cylindrical tanks, the top or bottom of manholes, glands, stuffing boxes, pipe flanges, and other similar structures. (Visit for Full Course or Watch Video Lecture here)

अण्डाकार आकृतियों का उपयोग मेहराबों, पुलों, बांधों, कपड़ा मशीनों के अण्डाकार गियर्स और प्रिंटिंग प्रेस, बेलनाकार टैंकों के सिरों, मैनहोल के ऊपर या नीचे, ग्रंथियों, स्टफिंग बॉक्स, पाइप फ्लैंगेस और अन्य समान संरचनाओं के निर्माण में किया जाता है।

General Method of Construction of Ellipse / दीर्घवृत्त के निर्माण की सामान्य विधि

To construct an ellipse when the distance of the focus from the directrix is equal to 50 mm and eccentricity is 2/3 (Visit for Full Course or Watch Video Lecture here)

(i) Draw any vertical line AB as directrix.
(ii) At any point C on it, draw the axis perpendicular to the AB (directrix).
(iii) Mark a focus F on the axis such that Cf = 50 mm.
(iv) Divide CF into 5 equal divisions (sum of numerator and denometer of the eccentricity).
(v) Mark the vertex V on the third division-point from C.
Thus, eccentricity, e = VF/VC= 2/3
(vi) A scale may now be constructed on the axis (as explained below), which will directly give the distances in the required ratio.
(vii) At V, draw a perpendicular VE equal to VF. Draw a line joining C and E. Thus, in triangle CVE, VE/VC=VF/VC=2/3
(viii) Mark any point 1 on the axis and through it, draw a perpendicular
to meet CE-produced at 1′.
(ix) With centre F and radius equal to 1-1 ‘, draw arcs to intersect the perpendicular through 1 at points P1 and P’1.
These are the points on the ellipse, because the distance of P1 from AB is equal to C1, P1 F = 1-1′ and 1-1’/C1=VF/VC=2/3
Similarly, mark points 2, 3 etc. on the axis and obtain points P2 and P’2 , P3 and P’3 etc.
(x) Draw the ellipse through these points. It is a closed curve having two foci and two directrices.

(i) नियता के रूप में कोई ऊर्ध्वाधर रेखा AB खींचिए।
(ii) इस पर किसी बिंदु C पर AB (डायरेक्ट्रिक्स) के लम्बवत् अक्ष खींचिए।
(iii) अक्ष पर फ़ोकस F इस प्रकार अंकित करें कि Cf = 50 मिमी।
(iv) CF को 5 बराबर भागों में विभाजित करें (उत्केन्द्रता के अंश और दाेनोमीटर का योग)।
(v) C से तीसरे विभाजन-बिंदु पर शीर्ष V अंकित करें।
अत: उत्केन्द्रता, e = VF/VC = 2/3
(vi) अब अक्ष पर एक पैमाना बनाया जा सकता है (जैसा कि नीचे बताया गया है), जो सीधे आवश्यक अनुपात में दूरियां देगा।
(vii) V पर, VF के बराबर लंब VE खींचिए। C और E को मिलाने वाली एक रेखा खींचिए। इस प्रकार, त्रिभुज CVE में, VE/VC=VF/VC=2/3
(viii) अक्ष पर कोई बिंदु 1 चिह्नित करें और इसके माध्यम से एक लंब खींचें
CE-उत्पादित 1′ पर मिलने के लिए।
(ix) F को केंद्र और 1-1′ के बराबर त्रिज्या लेकर, 1 से लंब को P1 और P’1 बिंदुओं पर काटने के लिए चाप लगाएं।
दीर्घवृत्त पर ये बिंदु हैं, क्योंकि AB से P1 की दूरी C1 के बराबर है, P1 F = 1-1′ और 1-1’/C1=VF/VC=2/3
इसी प्रकार, अक्ष पर 2, 3 आदि बिंदु अंकित करें और बिंदु P2 और P’2, P3 और P’3 आदि प्राप्त करें।
(x) इन बिन्दुओं से होकर एक दीर्घवृत्त खींचिए। यह एक बंद वक्र है जिसमें दो फोकस और दो डायरेक्ट्री हैं।

Construction of Ellipse by other methods / अन्य तरीकों से दीर्घवृत्त का निर्माण

Ellipse is also defined as a curve traced out by a point, moving in the same plane as and in such a way that the sum of its distances from two fixed points is always the same. (Visit for Full Course or Watch Video Lecture here)

(i) Each of the two fixed points is called the focus.
(ii) The line passing through the two foci and terminated by the curve, is called the major axis.
(iii) The line bisecting the major axis at right angles and terminated by the curve, is called the minor axis.
Conjugate axes: Those axes are called conjugate axes when they are parallel to the tangents drawn at their extremities.
In fig. 3.1 below, AB is the major axis, CD the minor axis and F1 and F2 are the foci. The foci are equidistant from the centre O.
The points A, P, C etc. are on the curve and hence, according to the definition, (AF1 + AF2) = (PF1 + PF2) = (C F1 + CF2) etc.
But (AF1 + AF2) = AB. :. (PF1 + PF2 ) = AB, the major axis.
Therefore, the sum of the distances of any point on the curve from the two foci is equal to the major axis.
Again, (CF1 + CF2) = AB. But CF1 = CF2 :. CF1 = CF2 =1/2 AB.
Hence, the distance of the ends of the minor axis from the foci is equal to half the major axis.

दीर्घवृत्त को एक बिंदु द्वारा खींचे गए वक्र के रूप में भी परिभाषित किया गया है, जो एक ही विमान में और इस तरह से चलता है कि दो निश्चित बिंदुओं से इसकी दूरियों का योग हमेशा समान होता है।
(i) दो निश्चित बिंदुओं में से प्रत्येक को फोकस कहा जाता है।
(ii) दो नाभियों से गुजरने वाली और वक्र द्वारा समाप्त होने वाली रेखा को दीर्घ अक्ष कहते हैं।
(iii) वह रेखा जो दीर्घ अक्ष को समकोण पर समद्विभाजित करती है और वक्र द्वारा समाप्त होती है, लघु अक्ष कहलाती है।
संयुग्मी अक्ष: वे अक्ष संयुग्मी अक्ष कहलाते हैं जब वे अपने सिरों पर खींची गई स्पर्श रेखाओं के समान्तर होते हैं।
अंजीर में। नीचे चित्र 3.1 में AB प्रमुख अक्ष है, CD लघु अक्ष है और F1 और F2 नाभियाँ हैं। Foci केंद्र O से समान दूरी पर हैं।
बिंदु A, P, C आदि वक्र पर हैं और इसलिए, परिभाषा के अनुसार, (AF1 + AF2) = (PF1 + PF2) = (C F1 + CF2) आदि।
परंतु (AF1 + AF2) = AB. :. (PF1 + PF2 ) = AB, दीर्घ अक्ष।
इसलिए, दो नाभियों से वक्र पर किसी भी बिंदु की दूरियों का योग प्रमुख अक्ष के बराबर होता है।
पुनः, (CF1 + CF2) = AB. परंतु CF1 = CF2 :. CF1 = CF2 = 1/2 AB।
अतः नाभियों से लघु अक्ष के सिरों की दूरी दीर्घ अक्ष के आधे के बराबर होती है।

Arcs of circles method /वृत्त विधि के चाप

(i) Draw a line AB equal to the major axis and a line CD equal to the minor axis, bisecting each other at right angles at O.
(ii) With centre C and radius equal to half AB (i.e. AO ) draw arcs cutting AB at F1 and F2, the foci of the ellipse.
(iii) Mark a number of points 1, 2, 3 etc. on AB.
(iv) With centres F1 and F2 and radius equal to A1, draw arcs on both sides of AB.
(v) With same centres and radius equal to B1, draw arcs intersecting the previous arcs at four points marked P1.
(vi) Similarly, with radii A2 and B2, A3 and B3 etc. obtain more points.
(vii) Draw a smooth curve through these points. This curve is the required ellipse. (Visit for Full Course or Watch Video Lecture here)

(i) प्रमुख अक्ष के बराबर एक रेखा AB और लघु अक्ष के बराबर एक रेखा CD खींचिए, जो O पर समकोण पर एक दूसरे को समद्विभाजित करती है।
(ii) C को केंद्र से लेकर आधे AB के बराबर त्रिज्या (अर्थात् AO) AB को दीर्घवृत्त की नाभियाँ F1 और F2 पर काटते हुए चाप लगाते हैं।
(iii) AB पर अनेक बिंदु 1, 2, 3 आदि अंकित कीजिए।
(iv) F1 और F2 को केंद्र और A1 के बराबर त्रिज्या लेकर AB के दोनों ओर चाप लगाइए।
(v) एक ही केंद्र और B1 के बराबर त्रिज्या के साथ, पिछले चापों को P1 चिह्नित चार बिंदुओं पर प्रतिच्छेद करते हुए चाप बनाएं।
(vi) इसी प्रकार, त्रिज्या A2 और B2, A3 और B3 आदि के साथ अधिक अंक प्राप्त करें।
(vii) इन बिन्दुओं से होकर एक चिकना वक्र खींचिए। यह वक्र आवश्यक दीर्घवृत्त है।

Concentric circles method / संकेंद्रित वृत्त विधि

(i) Draw the major axis AB and the minor axis CD intersecting each other at O.
(ii) With centre O and diameters AB and CD respectively, draw two circles.
(iii) Divide the major-axis-circle into a number of equal divisions, say 12 and mark points 1, 2 etc. as shown.
(iv) Draw lines joining these points with the centre O and cutting the minor-axis-circle at points 1 ‘, 2’ etc.
(v) Through point 1 on the major-axis-circle, draw a line parallel to CD, the minor axis.
(vi) Through point 1′ on the minor-axis-circle, draw a line parallel to AB, the major axis. The point P1, where these two lines intersect is on the required ellipse.
(vii) Repeat the construction through all the points. Draw the ellipse through A, P1, P2 . etc. 

(Visit for Full Course or Watch Video Lecture here)

(i) दीर्घ अक्ष AB और लघु अक्ष CD खींचिए जो परस्पर O पर प्रतिच्छेद करती है।
(ii) केंद्र O और व्यास AB और CD लेकर क्रमशः दो वृत्त खींचिए।
(iii) दीर्घ-अक्ष-वृत्त को कई समान भागों में विभाजित करें, मान लीजिए 12 और बिंदु 1, 2 आदि को चिन्हित करें जैसा कि दिखाया गया है।
(iv) इन बिंदुओं को केंद्र 0 से मिलाने वाली रेखाएँ खींचिए और लघु-अक्ष-वृत्त को बिंदुओं 1′, 2′ आदि पर काटिए।
(v) प्रमुख-अक्ष-वृत्त पर बिंदु 1 के माध्यम से, सीडी, लघु अक्ष के समानांतर एक रेखा खींचें।
(vi) लघु-अक्ष-वृत्त पर बिंदु 1′ के माध्यम से, प्रमुख अक्ष AB के समानांतर एक रेखा खींचें। बिंदु P1, जहाँ ये दो रेखाएँ प्रतिच्छेद करती हैं, आवश्यक दीर्घवृत्त पर है।
(vii) सभी बिन्दुओं पर रचना को दोहराइए। A, P1, P2 से होकर दीर्घवृत्त खींचिए। आदि।

Rectangle or Oblong Method / आयत या आयताकार विधि

(Visit for Full Course or Watch Video Lecture here)

(i) Draw the two axes AB and CD intersecting each other at O.
(ii) Construct the oblong EFGH having its sides equal to the two axes.
(iii) Divide the semi-major-axis AO into a number of equal parts, say 4, and AE into the same number of equal parts, numbering them from A as shown.
(iv) Draw lines joining 1 ‘, 2′ and 3’ with C.
(v) From D, draw lines through 1, 2 and 3 intersecting C’1, C’2 and C’3 at points P1, P2 and P3 respectively.
(vi) Draw the curve through A, P1 ….. C. It will be one quarter of the ellipse.
(vii) Complete the curve by the same construction in each of the three remaining quadrants.
As the curve is symmetrical about the two axes, points in the remaining quadrants may be located by drawing perpendiculars and horizontals from P1, P2 etc. and making each of them of equal length on both the sides of the two axes. For example, P2x = x P11 and P2y = yP5.

(i) O पर परस्पर प्रतिच्छेद करने वाली दो अक्ष AB और CD खींचिए।

(ii) आयताकार EFGH की रचना कीजिए, जिसकी भुजाएँ दोनों अक्षों के बराबर हों।
(iii) सेमी-मेजर-एक्सिस AO को कई समान भागों में विभाजित करें, मान लीजिए 4, और AE को समान भागों की समान संख्या में विभाजित करें, जैसा कि दिखाया गया है।
(iv) 1′, 2′ और 3′ को C से मिलाने वाली रेखाएँ खींचिए।
(v) D से, 1, 2 और 3 से होकर C’1, C’2 और C’3 को क्रमश: P1, P2 और P3 पर प्रतिच्छेद करती हुई रेखाएँ खींचिए।
(vi) A, P1…C से वक्र खींचिए। यह दीर्घवृत्त का एक चौथाई होगा।
(vii) शेष तीन चतुर्थांशों में से प्रत्येक में समान रचना द्वारा वक्र को पूरा करें।
चूंकि वक्र दो अक्षों के बारे में सममित है, शेष चतुर्भुजों में बिंदुओं को P1, P2 आदि से लंबवत और क्षैतिज खींचकर और उनमें से प्रत्येक को दो अक्षों के दोनों किनारों पर समान लंबाई बनाकर स्थित किया जा सकता है। उदाहरण के लिए, P2x = x P11 और P2y = yP5।

Loop of the thread method / थ्रेड विधि का लूप

This is practical application of the first method.
(i) Draw the two axes AB and CD intersecting at O. Locate the foci F1 and F2.
(ii) Insert a pin at each focus-point and tie a piece of thread in the form of a loop around the pins, in such a way that the pencil point when placed in the loop (keeping the thread tight), is just on the end C of the minor axis.
(iii) Move the pencil around the foci, maintaining an even tension in the thread throughout and obtain the ellipse.
It is evident that PF1 + PF2= CF1 + C F2 etc.

(Visit for Full Course or Watch Video Lecture here)

यह पहली विधि का व्यावहारिक अनुप्रयोग है।
(i) O पर प्रतिच्छेद करने वाली दो अक्ष AB और CD खींचिए। F1 और F2 नाभियों का पता लगाइए।
(ii) प्रत्येक फ़ोकस-बिंदु पर एक पिन लगाएँ और पिनों के चारों ओर धागे के एक टुकड़े को एक लूप के रूप में इस प्रकार बाँधें कि पेंसिल की नोक को जब लूप में रखा जाए (धागे को कस कर रखा जाए), ठीक ऊपर हो छोटी धुरी का अंत सी।
(iii) पूरे धागे में समान तनाव बनाए रखते हुए, पेंसिल को नाभियों के चारों ओर घुमाएं और दीर्घवृत्त प्राप्त करें।
यह स्पष्ट है कि PF1 + PF2 = CF1 + C F2 इत्यादि।

Trammel method / ट्रामेल विधि

(i) Draw the two axes AB and CD intersecting each other at O. Along the edge of a strip of paper which may be used as a trammel, mark PQ equal to half the minor axis and PR equal to half the major axis.
(ii) Place the trammel so that R is on the minor axis CD and Q on the major axis AB. Then P will be on the required ellipse. By moving the trammel to new positions, always keeping R on CD and Q on AB, obtain other points. Draw the ellipse through these points.

(i) O पर परस्पर प्रतिच्छेद करने वाली दो अक्ष AB और CD खींचिए। कागज की एक पट्टी के किनारे के साथ, जिसे ट्रामेल के रूप में इस्तेमाल किया जा सकता है, PQ को लघु अक्ष के आधे के बराबर और PR को आधे दीर्घ अक्ष के बराबर चिह्नित करें।
(ii) ट्रैमेल को इस प्रकार रखें कि R लघु अक्ष CD पर हो और Q दीर्घ अक्ष AB पर हो। तब P आवश्यक दीर्घवृत्त पर होगा। ट्रैमेल को नए स्थान पर ले जाकर, हमेशा R को CD पर और Q को AB पर रखते हुए, अन्य बिंदु प्राप्त करें। इन बिन्दुओं से दीर्घवृत्त खींचिए।

Construction of Parabola / परवलय (पैराबोला) का निर्माण

Use of parabolic curves is made in arches, bridges, sound reflectors, light reflectors etc. Mathematically a parabola can be described by an equation y^2 =4 ax or x^2 = 4a y.

परवलयिक वक्रों का उपयोग मेहराब, पुलों, ध्वनि परावर्तकों, प्रकाश परावर्तकों आदि में किया जाता है। गणितीय रूप से एक परवलय को एक समीकरण y^2 =4ax या x^2 = 4ay द्वारा वर्णित किया जा सकता है।

General method of construction of a parabola: / एक परवलय के निर्माण की सामान्य विधि:

To construct a parabola, when the distance of the Focus from the directrix is 50 mm. (Visit for Full Course or Watch Video Lecture here)

(i) Draw the directrix AB and the axis CD.
(ii) Mark focus F on CD, 50 mm from C.
(iii) Bisect CF in V the vertex (because eccentricity = 1 ).
(iv) Mark a number of points 1, 2, 3 etc. on the axis and through them, draw perpendiculars to it.
(v) With centre F and radius equal to C1, draw arcs cutting the perpendicular through 1 at P1 and P’1 .
(vi) Similarly, locate points P2 and P’2 , P3 and P’3 etc. on both the sides of the axis.
(vii) Draw a smooth curve through these points.
This curve is the required parabola. It is an open curve.

परवलय की रचना करने के लिए, जब नियता से फोकस की दूरी 50 मिमी हो।
(i) नियता AB और अक्ष CD खींचिए।
(ii) मार्क फोकस फॉन सीडी, सी से 50 मिमी।
(iii) शीर्ष V में CF को समद्विभाजित करें (क्योंकि उत्केन्द्रता = 1)।
(iv) अक्ष पर 1, 2, 3 आदि अनेक बिंदु अंकित कीजिए और उनसे लंब खींचिए।
(v) F को केंद्र और C1 के बराबर त्रिज्या लेकर, 1 से P1 और P’1 पर लंब काटने वाले चाप लगाएं।
(vi) इसी प्रकार अक्ष के दोनों ओर बिंदुओं P2 और P’2, P3 और P’3 आदि को अंकित कीजिए।
(vii) इन बिन्दुओं से होकर एक चिकना वक्र खींचिए।
यह वक्र अभीष्ट परवलय है। यह एक खुला वक्र है।

Construction of parabola by other methods: / अन्य विधियों द्वारा परवलय का निर्माण:

Rectangle method / आयताकार विधि

To construct a parabola given the base and the axis. (Visit for Full Course or Watch Video Lecture here)

(i) Draw the base AB.
(ii) At its mid-point E, draw the axis EF at right angles to AB.
(iii) Construct a rectangle ABCD, making side BC equal to EF.
(iv) Divide AE and AD into the same number of equal parts and name them as shown (starting from A).
(v) Draw lines joining F with points 1, 2 and 3. Through 1 ‘, 2′ and 3’, draw perpendiculars to AB intersecting F1, F2 and F3 at points P1, P2 and P3 respectively.
(vi) Draw a curve through A, P1, P2 etc. It will be a half parabola.
Repeat the same construction in the other half of the rectangle to complete the parabola. Or, locate the points by drawing lines through the points P1, P2 etc. parallel to the base and making each of them of equal length on both the sides of EF, e.g. P1O = OP’1 . AB and EF are
called the base and the axis respectively of the parabola.

आधार और अक्ष को देखते हुए एक परवलय का निर्माण करना।
(i) आधार AB खींचिए।
(ii) इसके मध्य-बिन्दु E पर AB के समकोण पर अक्ष EF खींचिए।
(iii) भुजा BC को EF के बराबर बनाते हुए एक आयत ABCD की रचना कीजिए।
(iv) AE और AD को समान भागों में विभाजित करें और दिखाए गए अनुसार उन्हें नाम दें (A से शुरू करते हुए)।
(v) बिंदु 1, 2 और 3 के साथ F को मिलाने वाली रेखाएँ खींचें। 1 ‘, 2′ और 3’ के माध्यम से AB पर लंबवत रेखाएँ खींचें, जो F1, F2 और F3 को क्रमशः बिंदुओं P1, P2 और P3 पर काटती हैं।
(vi) A, P1, P2 आदि के माध्यम से एक वक्र बनाएं। यह एक आधा परवलय होगा।
पैराबोला को पूरा करने के लिए आयत के दूसरे भाग में उसी निर्माण को दोहराएं। या, बिंदुओं P1, P2 आदि के माध्यम से आधार के समानांतर रेखाएं खींचकर बिंदुओं का पता लगाएं और उनमें से प्रत्येक को EF के दोनों किनारों पर समान लंबाई का बनाएं, उदा। P1O = OP’1। AB और EF हैं
परवलय का क्रमशः आधार और अक्ष कहते हैं।

Tangent method / स्पर्शरेखा विधि

(i) Draw the base AB and the axis EF. (These are taken different from those in rectangle method.)

Parabola: Tangent Method (Visit for Full Course or Watch Video Lecture here)

(ii) Produce EF to O so that EF = FO.
(iii) Join O with A and B. Divide lines OA and OB into the same number of equal parts, say 8.
(iv) Mark the division-points as shown in the figure.
(v) Draw lines joining 1 with 1 ‘, 2 with 2’ etc. Draw a curve starting from A and tangent to lines 1-1 ‘, 2-2’ etc. This curve is the required parabola.

(i) आधार AB और अक्ष EF खींचिए। (इन्हें आयत विधि से अलग लिया गया है।)
(ii) EF को O तक बढ़ाएँ ताकि EF = FO हो।
(iii) O को A और B से मिलाएं। रेखाओं OA और OB को समान भागों में विभाजित करें, मान लीजिए 8।
(iv) विभाजन-बिंदुओं को चित्र में दर्शाए अनुसार चिन्हित करें।
(v) 1 को 1′, 2 को 2′ आदि से मिलाने वाली रेखाएँ खींचिए। A से प्रारंभ होकर 1-1′, 2-2′ आदि रेखाओं को स्पर्श करने वाला वक्र खींचिए। यह वक्र आवश्यक परवलय है।

Construction of Hyperbola / हाइपरबोला का निर्माण

Use of hyperbolical curves is made in cooling towers, water channels etc.
Rectangular hyperbola: It is a curve traced out by a point moving in such a way that the product of its distances from two fixed lines at right angles to each other is a constant. The fixed lines are called asymptotes.
This curve graphically represents the Boyle’s Law, viz. P x V = a, P = pressure, V = volume and a is constant. It is also useful in design of water channels.

कूलिंग टावर्स, वॉटर चैनल्स आदि में हाइपरबोलिकल कर्व्स का इस्तेमाल किया जाता है।
आयताकार अतिपरवलय: यह एक वक्र है जो एक बिंदु द्वारा इस तरह से चलता है कि एक दूसरे से समकोण पर दो निश्चित रेखाओं से इसकी दूरियों का गुणनफल एक स्थिर होता है। निश्चित रेखाओं को स्पर्शोन्मुख कहा जाता है।
यह वक्र ग्राफिक रूप से बॉयल के नियम का प्रतिनिधित्व करता है, अर्थात। P x V = a, P = दबाव, V = आयतन और a स्थिर है। यह जल चैनलों के डिजाइन में भी उपयोगी है।

General method of construction of a hyperbola: / अतिपरवलय के निर्माण की सामान्य विधि:

Construct a hyperbola, when the distance of the focus from the directrix is 65 mm and eccentricity is 3/2 (Visit for Full Course or Watch Video Lecture here)
(i) Draw the directrix AB and the axis CD.
(ii) Mark the focus F on CD and 65 mm from C.
(iii) Divide CF into 5 equal divisions and mark V the vertex, on the second division from C. Thus, eccentricity = VF/VC=3/2
To construct the scale for the ratio 3/2 draw a line VE perpendicular to CD such that VE = VF. Join C with E. Thus, in triangle CVE, VE/VC = VF/VC=3/2
(iv) Mark any point 1 on the axis and through it, draw a perpendicular to meet CE-produced at 1 ‘.
(v) With centre F and radius equal to 1-1 ‘, draw arcs intersecting the perpendicular through 1 at P1 and P’1·
(vi) Similarly, mark a number of points 2, 3 etc. and obtain points P2 and P’2 , P3 and P’3 etc.
(vii) Draw the hyperbola through these points.

एक अतिपरवलय की रचना करें, जब नियता से फोकस की दूरी 65 मिमी और उत्केन्द्रता 3/2 हो
(i) नियता AB और अक्ष CD खींचिए।
(ii) सीडी पर फोकस एफ और सी से 65 मिमी चिह्नित करें।
(iii) CF को 5 बराबर भागों में विभाजित करें और C से दूसरे भाग पर शीर्ष V को चिन्हित करें। इस प्रकार, उत्केन्द्रता = VF/VC=3/2
अनुपात 3/2 के लिए पैमाने का निर्माण करने के लिए सीडी के लिए एक रेखा VE लंबवत बनाएं जैसे कि VE = VF। C को E से मिलाइए। इस प्रकार, त्रिभुज CVE में, VE/VC = VF/VC=3/2
(iv) अक्ष पर कोई बिंदु 1 चिह्नित करें और इसके माध्यम से, सीई-उत्पादित 1′ पर मिलने के लिए एक लंब बनाएं।
(v) केंद्र F और 1-1′ के बराबर त्रिज्या के साथ, P1 और P’1· पर 1 से लंब को काटते हुए चाप बनाएं।
(vi) इसी प्रकार, अंक 2, 3 इत्यादि को चिह्नित करें और P2 और P’2, P3 और P’3 आदि अंक प्राप्त करें।
(vii) इन बिन्दुओं से होकर अतिपरवलय खींचिए।

Construction of Hyperbola by other method / अन्य विधि द्वारा हाइपरबोला का निर्माण

To draw a hyperbola when its foci and vertices are given, and to locate its asymptotes / एक अतिपरवलय की रचना करना जब इसके फोकस और शीर्ष दिए गए हों, और इसके स्पर्शोन्मुखों का पता लगाना।

(i) Draw a horizontal line as axis and on it, mark the given foci F and F1, and vertices V and V1 .
(ii) Mark any number of points 1, 2, 3 etc. to the right of F1 .
(iii) With F and F1 as centres and radius, say V2, draw four arcs.
(iv) With the same centres and radius V12, draw four more arcs intersecting the first four arcs at points P2• Then these points lie on the hyperbola.
(v) Repeat the process with the same centres and radii V1 and V11, V3 and V13 etc. Draw the required hyperbola through the points thus obtained.
(vi) With FF1 as diameter, draw a circle.
(vii) Through the vertices V and V1, draw lines perpendicular to the axis, cutting the circle at four points A. From O, the centre of the circle, draw lines passing through points A. These lines are the required asymptotes.

(Visit for Full Course or Watch Video Lecture here)

(i) अक्ष के रूप में एक क्षैतिज रेखा खींचिए और उस पर दिए गए नाभियाँ F और F1, और शीर्ष V और V1 अंकित कीजिए।
(ii) F1 के दाईं ओर कितने भी बिंदु 1, 2, 3 आदि अंकित करें।
(iii) F और F1 को केंद्र मानकर और त्रिज्या, मान लीजिए V2, से चार चाप लगाइए।
(iv) उसी केंद्र और त्रिज्या V12 से, चार और चाप खींचिए जो पहले चार चापों को बिंदु P2 पर प्रतिच्छेद करते हैं • फिर ये बिंदु अतिपरवलय पर स्थित होते हैं।
(v) समान केंद्रों और त्रिज्या V1 और V11, V3 और V13 आदि के साथ प्रक्रिया को दोहराएं। इस प्रकार प्राप्त बिंदुओं के माध्यम से आवश्यक अतिपरवलय बनाएं।
(vi) FF1 को व्यास मानकर एक वृत्त खींचिए।
(vii) शीर्षों V और V1 से, वृत्त को चार बिंदुओं A पर काटते हुए, अक्ष के लम्बवत् रेखाएँ खींचें। वृत्त के केंद्र O से, बिंदु A से होकर जाने वाली रेखाएँ खींचें। ये रेखाएँ आवश्यक अनंतस्पर्शी रेखाएँ हैं।

Construction of Rectangular Hyperbola / आयताकार हाइपरबोला का निर्माण

To draw a rectangular hyperbola, given the position of a point P on it.
(i) Draw lines OA and OB at right angles to each other.
(ii) Mark the position of the point P.
(iii) Through P, draw lines CD and EF parallel to OA and OB respectively.
(iv) Along PD, mark a number of points 1, 2, 3 etc. not necessarily
equidistant.
(v) Draw lines O1, O2 etc. cutting PF at points 1 ‘, 2’ etc.
(vi) Through point 1, draw a line parallel to OB and through 1′, draw a
line parallel to OA, intersecting each other at a point P1.
(vii) Obtain other points in the same manner.
For locating the point, say P6, to the left of P, the line O6 should be extended to meet PE at 6′. Draw the hyperbola through the points P6, P, P1 etc.
A hyperbola, through a given point situated between two lines making any angle between them, can similarly be drawn, as shown in figure.

(Visit for Full Course or Watch Video Lecture here)

एक आयताकार अतिपरवलय बनाने के लिए, उस पर बिंदु P की स्थिति दी गई है।
(i) OA और OB समकोण पर रेखाएँ खींचिए।
(ii) बिंदु P की स्थिति अंकित करें।
(iii) P से होकर क्रमशः OA और OB के समांतर रेखाएँ CD और EF खींचिए।
(iv) PD के साथ-साथ 1, 2, 3 आदि कुछ बिंदु अवश्य अंकित करें
समदूरस्थ।
(v) पीएफ को बिंदु 1′, 2′ आदि पर काटती हुई रेखाएँ O1, O2 आदि खींचिए।
(vi) बिंदु 1 से OB के समानांतर एक रेखा खींचिए और 1′ से a खींचिए
OA के समानांतर रेखा, एक दूसरे को बिंदु P1 पर प्रतिच्छेद करती है।
(vii) इसी तरह अन्य बिंदु प्राप्त करें।
बिंदु का पता लगाने के लिए, मान लीजिए P6, P के बाईं ओर, लाइन O6 को PE को 6′ पर मिलने के लिए बढ़ाया जाना चाहिए। बिंदुओं P6, P, P1 आदि से होकर अतिपरवलय खींचिए।
एक अतिपरवलय, उनके बीच कोई कोण बनाने वाली दो रेखाओं के बीच स्थित एक दिए गए बिंदु के माध्यम से इसी तरह खींचा जा सकता है, जैसा कि चित्र में दिखाया गया है।

Drawing Tangents and Normals to Conic Section Curves / शांकव धारा वक्रों के लिए स्पर्शरेखा और सामान्य बनाना

General Method

The common rule for drawing tangents and normals:
When a tangent at any point on the curve is produced to meet the directrix, the line joining the focus with this meeting point will be at right angles to the line joining the focus with the point of contact. The normal to the curve at any point is perpendicular to the tangent at that point.

स्पर्शरेखा और मानक बनाने का सामान्य नियम:
जब वक्र के किसी भी बिंदु पर एक स्पर्शरेखा को नियता से मिलने के लिए बढ़ाया जाता है, तो इस मिलन बिंदु से फोकस को मिलाने वाली रेखा जुड़ने वाली रेखा के समकोण पर होगी संपर्क के बिंदु के साथ फोकस। किसी भी बिंदु पर वक्र के लिए सामान्य उस बिंदु पर स्पर्शरेखा के लंबवत होता है।

To draw a tangent at any point P on the conics (General Method of Construction of Ellipse, Parabola and Hyperbola)

(i) Join P with F.
(ii) From F, draw a line perpendicular to PF to meet AB at T.
(iii) Draw a line through T and P. This line is the tangent to the curve.
(iv) Through P, draw a line NM perpendicular to TP. NM is the normal to the curve.

(i) P को F से मिलाइए।
(ii) F से PF पर एक लंब रेखा खींचिए जो AB को T पर मिले।
(iii) T और P से होकर एक रेखा खींचिए। यह रेखा वक्र की स्पर्श रेखा है।
(iv) P से होकर TP पर NM लंब रेखा खींचिए। एनएम वक्र के लिए सामान्य है।

Other methods of drawing tangents to conics:/शांकवों पर स्पर्श रेखाएँ खींचने की अन्य विधियाँ:

Method I: To draw a tangent to an ellipse at any point P on it. / विधि I: दीर्घवृत्त के किसी बिंदु P पर स्पर्श रेखा खींचना।

(i) With O, the centre of the ellipse as centre, and one half the major axis as radius, draw a circle.
(ii) From P, draw a line parallel to the minor axis, cutting the circle at a point Q.
(iii) Draw a tangent to the circle at the point Q cutting the extended major axis at a point R.
From R, draw a line RS passing through P. RS is the required tangent to the ellipse.

(i) दीर्घवृत्त के केंद्र O को केंद्र मान कर और आधे दीर्घ अक्ष को त्रिज्या मानकर एक वृत्त खींचिए।
(ii) P से लघु अक्ष के समानांतर एक रेखा खींचिए, जो वृत्त को बिंदु Q पर काटती है।
(iii) विस्तारित दीर्घ अक्ष को बिंदु R पर काटते हुए बिंदु Q पर वृत्त की स्पर्श रेखा खींचिए।
R से, P से होकर जाने वाली एक रेखा RS खींचिए। RS दीर्घवृत्त की आवश्यक स्पर्श रेखा है।

Method II: When an axis of parabola is given / विधि II: जब परवलय का एक अक्ष दिया जाता है।

To draw a tangent to a parabola at any point P on it. / किसी परवलय के किसी बिन्दु P पर स्पर्श रेखा खींचना।

(i) From P, draw a perpendicular PA to the axis, intersecting it at a point A. Mark a point B on the axis such that BV = VA. Draw a line from B passing through P. Then this line is the required tangent. (Figure a)
(ii) Through P, draw a line PQ parallel to the axis. Draw two lines AB and CD parallel to, equidistant from and on opposite sides of PQ, and cutting the parabola at points A and C. Draw a line joining A with C.
Through P, draw a line RS parallel to AC. RS is the required tangent. (Figure b)

(i) P से, अक्ष पर एक लंब PA खींचिए, जो इसे बिंदु A पर प्रतिच्छेद करे। अक्ष पर एक बिंदु B इस प्रकार अंकित कीजिए कि BV = VA हो। B से P से होकर जाने वाली एक रेखा खींचिए। तब यह रेखा अभीष्ट स्पर्श रेखा है।
(ii) P से होकर अक्ष के समांतर एक रेखा PQ खींचिए। दो रेखाएँ AB और CD समानांतर, PQ से समान दूरी पर और विपरीत दिशा में खींचिए, और परवलय को बिंदुओं A और C पर काटिए। A को C से मिलाने वाली एक रेखा खींचिए।
P से होकर AC के समांतर एक रेखा RS खींचिए। RS अभीष्ट स्पर्श रेखा है।

Method III: When the focus and the directrix are given /विधि III: जब फ़ोकस और नियता दिए गए हों 

(i) From P draw a line PE perpendicular to the directrix AB, meeting it at a point F.
(ii) Draw a line joining P with the focus F.
(iii) Draw the bisector RS of angle EPF.
Then RS is the required tangent (Figure c).

(i) P से नियता AB पर लंबवत एक रेखा PE खींचिए, जो इसे बिंदु f पर मिले।
(ii) P को F फोकस से मिलाने वाली एक रेखा खींचिए।
(iii) कोण EPF का समद्विभाजक RS खींचिए।
तब RS अभीष्ट स्पर्श रेखा है।