Preferred Series Numbers in Machine Design

You are currently viewing Preferred Series Numbers in Machine Design

Preferred Series Numbers in Machine Design

Preferred Series Numbers in Machine Design and Drawing

What is Preferred Series Numbers?

The Preferred Series Number is a designed machine component that needs standardization to avoid variations. It implies that the product’s important parameters should be common in nature. For example, the sizes of the ingots (Raw Material) available in the market have standard sizes. A manufacturer does not produce ingots of sizes of his wish, he must follow a definite pattern to produce the ingots in that size. The designer can choose the dimensions from those standard available sizes.

Motor speed, the engine power of a tractor, machine tool speed and feed, all follow a definite pattern or series. This also helps in the interchangeability of products. It has been shown by experience that if the sizes are put in the form of geometric progression, then wide ranges are covered with a definite sequence.

These numbers are called preferred series numbers having common ratios as,

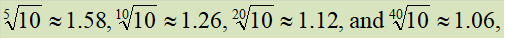
Depending on the common ratio, four basic series are formed; these are R5, R10, R20 and R40. These are named as Renard series (French balloonist and engineer Charles Renard). Many other derived series are formed by multiplying or dividing the basic series by 10, 100 etc. Typical values of the common ratio for the four basic Geometric Progression series are given below.

Examples of R5/R10/R20/R40 Number Series

  • R10, R20 and R40: Thickness of sheet metals, wire diameter.
  • R5, R10, R20: Speed, layout in a machine tool (R10: 1000,1250,1600, 2000)
  • R20 or R40: Machine tool feed.

The hoisting capacities (in tonnes) of cranes are in R10 series, while the hydraulic cylinder diameters are in R40 series and hydraulic cylinder capacities are in R5 series. Wire diameter of helical springs are in R20 series.

 

Types of Preferred Series

There are two types of series Basic Number Series and Derived Number Series and derived series are further divided into Method 1 and Method 2.

Basic series of preferred numbers

“R5, R10, R20, R40 and R80 are called basic series.”

Any series that is formed based on these five basic series is called derived series.

Derived series of preferred numbers

There are two methods of forming derived series, namely, reducing the numbers of a particular basic series or increasing the numbers.

Methods of Forming Derived Series(Derived Series in Machine Design)

Method 1

In the first method, a derived series is obtained by taking every second, third, fourth or pth term of a given basic series. Such a derived series is designated by the symbol of the basic series followed by the number 2, 3, 4 or p and separated by ‘/’ sign.

If the series is limited, the designation also includes the limits inside the bracket. If the series is unlimited, at least one of the numbers of that series is mentioned inside the bracket.

Let us consider the meaning of these designations.

(i) Series R 10/3 (1, …,1000) indicates a derived series comprising of every third term of the R10 series and having the lower limit as 1 and a higher limit as 1000.

(ii) Series R 20/4 (…, 8, …) indicates a derived series comprising of every fourth term of the R20 series, unlimited in both sides and having the number 8 inside the series.

(iii) Series R 20/3 (200, …) indicates a derived series comprising of every third term of the R20 series and having the lower limit as 200 and without any higher limit.

(iv) Series R 20/3 (…200) indicates a derived series comprising of every third term of the R20 series and having the higher limit as 200 and without any lower limit.

Read more topics and video tutorials on Machine Design & Drawing

Method 2

In the second method, the derived series is obtained by increasing the numbers of a particular basic series. Let us consider an example of a derived series of numbers ranging from 1 to 1000 based on the R5 series.

  • The numbers belonging to the R5 series from 1 to 10 are as follows: 1, 1.6, 2.5, 4, 6.3, 10
  • The next numbers are obtained by multiplying the above numbers by 10 are as follows: 16, 25, 40, 63, 100
  • The same procedure is repeated, and the next numbers are obtained by multiplying the above numbers by 10 are 160, 250, 400, 630, 1000

Therefore, the complete derived series based on R5 series is as follows: 1, 1.6, 2.5, 4, 6.3, 10, 16, 25, 40, 63, 100, 160, 150, 400, 630, 1000

The advantage of derived series is that one can obtain geometric series for any range of numbers, that is, with any value of the first and the last numbers. Also, one can have any intermediate numbers between these two limits.

References

  • ABDULLA SHARIF, Design of Machine Elements, Dhanpat Rai Publications (P) Ltd, New Delhi, 1995
  • V. B. Bhandari, Design of Machine Elements, Third Ed., The McGraw-Hills Companies, New Delhi
  • R. S. KHURMI and J.K. GUPTA, A Text-Book of Machine Design, S.Chand and company ltd., New Delhi, 2000. Design of Machine Elements https://nptel.ac.in/courses/112/105/112105125/

Q & A

  1. Find out the numbers of the R5 basic series from 1 to 25.

  2. Find out the numbers of R20/4 (100, . . . . . . . . . . , 1000)derived series.

  3. A manufacturer is interested in starting a business with five different models of tractors ranging from 7.5 to 75 kW capacities. Specify the power capacities of the models. There is an expansion plan to further increase the number of models from five to nine to fulfil the requirement of farmers. Specify the power capacities of the additional models.

  4. It is required to standardize eleven shafts from 100 to 1000 mm diameter. Specify their diameters.

 

Leave a Reply